Sabemos que la membrana funciona frente a voltajes hiperpolarizantes y a algunos despolarizantes menores como una resistencia simple, es decir, de una manera linea, si aumentamos la corriente, se aumentará el voltaje de una manera proporcional (Figura 1). Sin embargo, si se analiza la duración temporal no responde de igual forma.
Figura1: Relación entre corriente y voltaje. A, el aumento de las pulsaciones de corriente hacia fuera o hacia dentro, producen cambios proporcionales y simétricos en Vm. B. se obtiene una curva I-V (en este caso lineal) que representa el voltaje en estado estacionario y la corriente inyectada.
Una verdadera resistencia responde a un modificación de la corriente con un cambio similar en el potencial de membrana, o sea, si damos un pulso cuadrado de corriente a nuestra célula, deberíamos ver un aumento o disminución cuadrada de voltaje (figura 2) sin embargo, en el caso de una célula esto no ocurre así ya que la respuesta de voltaje varía más lentamente que el cambio de corriente. Este retraso generado en la estabilización del Vm luego de haber dado el el pulso de corriente, se debe a la capacitancia.
Figura 2: representación de un aumento instantáneo (resaltado en lineas negras en la figura A2) del potencial de membrana.
Figura 2: representación de un aumento instantáneo (resaltado en lineas negras en la figura A2) del potencial de membrana.
Para comprender cómo la capacitancia reduce la respuesta del voltaje, es necesario recordar que el voltaje a través de un condensador como la membrana celular es proporcional a la carga almacenada en éste:
donde Q (culombios) es la carga almacena y C es la capacitancia (faradios).
Para alterar el voltaje, debe añadirse o quitarse carga del condensador, por lo tanto,
El cambio de carga es el resultado de un flujo de corriente a través del codensador. A su vez, la corriente se define como
La magnitud del cambio de voltaje a través de un condensado en respuesta a una pulsación de corriente, dependerá del tiempo que dure esa corriente ya que se necesita de tiempo para que se depositen y se eliminen las cargas del condensador.
Además, la capacitancia es directamente proporcional al área de las placas de un condensador (recuerde que para el caso de una célula, los medios intra y extracelular forman los conductores, la bicapa forma el aislante, mientras que todo el conjunto forma el condensador). Así, cuanto mayor sea el área de un condensador, más carga almacenará para poder conseguir una diferencia de potencial determinada y por ende mientras mayor sea el tamaño de una célula más corriente se necesitará para producir el mismo estímulo que en una célula pequeña.
La ecuación mostrada arriba nos dice que el voltaje va a aumentar constantemente mientras dure el pulso de corriente, sin embargo, esto no es así. ¿Por qué?.
La corriente total que cruza la membrana está determinada por la corriente que cruza por los canales (corriente iónica) y al movimiento de cargas, las que se almacenan tanto en la cara externa como en la interna de la membrana, esta corriente se conoce como corriente capacitiva. Así:
donde Im es la corriente de membrana, Ii es la corriente iónica e Ic es la corriente capacitiva.
Dado que la resistencia y la capacitancia están en paralelo, ya que la corriente que atraviesa la membrana puede fluir tanto por los canales iónicos (resistencia) como por el condensador, el voltaje a través de cada elemento debe ser siempre el mismo e igual al potencial de membrana. Ahora, imaginemos que el potencial de membrana es cero mV y que en el momento T=0, aplicamos un pulso de corriente de una magnitud Im. Al principio, el voltaje a través de la resistencia y del condensador, es cero. Luego, como la corriente iónica se encuentra con la resistencia de los canales, al principio no circulará corriente por ellos siendo Ic igual a cero, sin embargo, la corriente capacitiva comienza a aumentar de manera instantánea, por lo tanto,
Además, a medida que aumenta la diferencia de potencial, Vm, gracias a la corriente capacitiva, se comienza a transportar corriente a través de las resistencias (canales iónicos). De este modo, al aumentar la corriente iónica, comienza a disminuir la corriente capacitiva (ver figura 3).
Figura 3: Corriente total de membrana (Im) y sus componentes iónicos y capacitivos.
Finalmente, cuando el pulso de corriente se acaba, la corriente de membrana es igual a cero, por lo que los canales dejan de transportar iones y las "placas del condensador" se deben descargar. Por este motivo, al final del pulso vemos una corriente capactiva opuesta a la que se obtuvo al principio. Además, sin aplicación de corriente, la carga del condensador se disipa, fluyendo alrededor del circuito a través de la vía de resistencia y el potencial de membrana, vuelve a cero.
La fase de ascenso del cambio de potencial se puede describir con la siguiente ecuación:
en la que e, que tiene un valor cercano a 2,72, es la base del sistema de logaritmos naturales y t es la constante temporal de la membrana, que equivale a
La constante temporal puede medirse experimentalmente y corresponde al tiempo que tarda el potencial de membrana en lograr el 63% de su valor en estado estacionario.




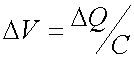

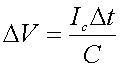





Muchas gracias me ha servido mucho de ayuda tu entrada del blog ^^
ResponderEliminarMe alegro mucho Nozomi. La verdad es que hace tiempo que no publico, porque los compromisos laborales han sido más de los que pensé. De todos modos, espero retomarlo pronto. Saludos!
ResponderEliminarHola, acabo de conocer el blog, me ha parecido muy interesante.
ResponderEliminarTengo una duda con respecto a la resistencia de membrana, en estos registros (http://oi47.tinypic.com/x2t7p4.jpg), el B presenta mayor resistencia ya que la curva de voltaje es menor¿?¿?
Agradezco me ayudes con eso...
Saludos desde Uruguay
Hola Ajedrez... disculpa la demora en la respuesta, pero bueno, me ha tocado un mes complicado. La diferencia principal que ves entre ambos registros, es la cinética de activación y deactivación. Me gustaría que me enviaras más información sobre la figura para aclarar mejor duda.
ResponderEliminarBuenísimo! Muchas gracias
ResponderEliminarUff excelente explicación! Gracias
ResponderEliminar