El objetivo de Hodgkin y Huxley (H-H) era encontrar los mecanismos moleculares para la generación del flujo iónico y los cambios de permeabilidad. Ellos describieron empíricamente bases que pueden resultar bastante simples pero que fueron muy útiles a la hora de predecir de manera correcta las principales formas de excitabilidad, así como la generación del potencial de acción y la velocidad de conducción.
El modelo de H-H separa las ecuaciones para la conductancia del sodio, gNa y potasio, gK. En cada caso se asume el límite superior de conductancia, así , gNa y gK son expresadas como conductancias máximas.
La dependencia del tiempo para gK es fácil de describir. En despolarización, el incremento de la conductancia del potasio sigue una forma sigmoidal a través del tiempo, mientras que en la repolarización decrece de forma exponencial (figura 1).
Figura 1: Curso temporal de los cambios en las conductancias de sodio y potasio durante un paso de despolarización a -9 mV. Las líneas cortadas muestran como la conductancia de sodio desminuye rápidamente al nivel de reposo si la membrana es repolarizada a - 65 mV en 0.63 mseg cuando la conductancia de sodio es máxima y como la conductancia de potasio disminuye más lentamente si la membrana es repolarizada luego de 6.3 mseg cuando la conductancia es máxima. Imagen tomada de Hille, B. (2001). Ion channels of excitable membranes, 3rd edn (Sunderland, Mass., Sinauer).
Tal como H y H notan, cada cinética puede ser obtenida si la apertura de un canal de K es controlado por partículas independientes unidas a la membrana. Ellos suponen que éstas serían cuatro partículas idénticas y que cada una de ellas presentaría una probabilidad “n” de ubicarse de manera correcta para conseguir un canal en estado abierto, por lo tanto, la posibilidad que “n” partículas estén correctamente ubicadas sería n4. Además, ya que la apertura de los canales de potasio depende del potencial de membrana, H-H especulan que estas hipotéticas partículas llevarían una carga eléctrica asociada, la cual haría que su distribución en la membrana sea voltaje dependiente. Suponen además, que cada partícula se mueve entre su posición permisiva y no permisiva (canal abierto-cerrado) con una cinética de primer orden. La figura 2, muestra que si “n” aumenta exponencialmente desde cero, “n4” aumenta en forma sigmoidea, imitando el lento incremento de la conductancia real de potasio en despolarización, mientras que si “n” cae exponencialmente a cero, n4 también cae exponencialmente ajustándose de mejor manera al decrecimiento de la conductancia de potasio en la repolarización.
Figura 2: Curso temporal de los parámetros del modelo H-H. Imagen tomada de Hille, B. (2001). Ion channels of excitable membranes, 3rd edn (Sunderland, Mass., Sinauer)
donde los cambios de n, dependientes del tiempo y voltaje se dan por una reacción de primer orden:
donde las partículas de gating “n” presentan transiciones entre la forma permisiva (canal abierto) y no permisiva (canal cerrado) con unas constantes de voltaje dependientes de an y bn por medio de una simple ecuación
Como la conductancia se presenta sólo cuando las cuatro partículas están abiertas o en posición “n” comportándose de forma independiente, la conductancia será proporcional al producto n por n por n por n, o
Además, en estado estacionario, es posible calcular la constante de tiempo dependiente de voltaje, tn y los valores de “n”, los cuales se definen como:


El modelo de H-H usa un formalismo similar para describir la INa , con cuatro hipotéticas partículas de gating, haciendo transiciones entre posiciones permisivas y no permisivas para controlar el canal. Sin embargo, ya que este canal presenta dos procesos opuestos: ACTIVACIÓN e INACTIVACIÓN, se presentan dos tipos de partículas diferentes. H-H las llamaron “m” y “h”, donde tres partículas “m” controlarían la activación, mientras que una partícula “h” controlaría la inactivación. Así, la probabilidad que ellos estén todos en posición permisiva es m3h y la corriente de sodio se representa como:
La figura 2, muestra cómo los cambios de m3h imitan la gNa a través del tiempo, durante y después del pulso de prueba. Durante la despolarización “m” crece rápidamente y “h” cae lentamente. Cuando m está al cubo (“m3”) se presenta un pequeño retraso en el aumento y al multiplicarlo por “h” que decae lentamente, m3h cae a valores muy bajos. Luego de la despolarización, “m” se recupera rápidamente y “h” lentamente, hasta alcanzar su valores originales. Al igual que en el caso del parámetro “n” del canal de potasio, “m” y “h” son asumidas por sufrir transiciones de primer orden entre las formas permisivas y no permisivas. De lo que se generan las siguientes ecuaciones:
donde
Los principales rasgos de los parámetros dependientes de voltaje se resumen en la figura 3. En esta figura, los valores para m, n y h en estado estacionario y las constantes de tiempo, están graficadas en función del potencial de membrana. Los puntos a recalcar son:
- las constantes de tiempo del proceso m son aproximadamente 10 veces más rápidas que la de los procesos n y h.
- los tres proceso son sigmoidales en V (voltaje) en el estado estacionario y tanto m como n (activación del canal de sodio y de potasio, respectivamente) aumentan con la despolarización, mientras que h (inactivación de sodio) disminuye.
- las constantes de tiempo son funciones de tipo campana con respecto al voltaje con la tendencia general a hacerse más rápidas durante despolarizaciones o hiperpolarizaciones extremas.

Figura 3: La dependencia de voltaje de las tres variables de estado y las constantes de tiempo del modelo H-H, desde el axón gigante de calamar a 6.3 ºC. Estos cambios dan una excelente descripción de los cambios de conductancia medidas bajo voltage clamp. Imagen tomada de Hille, B. (2001). Ion channels of excitable membranes, 3rd edn (Sunderland, Mass., Sinauer)
En la mayoría de la membranas biológicas, la membrana axonal contiene una conductancia de fuga o leak GL, la cual no depende del voltaje aplicado y permanece constante todo el tiempo.
donde gL es la conductancia leak.
Así, en resumen, el gran logro de Hodgkin y Huxley fue que su descripción clásica de las corrientes iónicas del axón gigante de calamar separó las conductancias en dos tipos: conductancia de sodio y de potasio. Estas conductancias quedan caracterizadas por su:
- Selectividad iónica.
- Dependencia de potencial de membrana.
Estas dos propiedades fueron separadas en la descripción matemática presentada por H-H. Así, por ejemplo, en el caso de la conductancia de potasio, n4, representa la parte dependiente del voltaje mientras que gK representa la conductancia máxima al potasio.
Hoy sabemos que las corrientes medidas por Hodgkin y Huxley son resultados de millones de canales iónicos en paralelo y selectivos a sodio o a potasio que se abren y cierran en forma aleatoria y en los que el tiempo de apertura y cierre está determinado por el potencial de membrana.



.PNG)



.PNG)
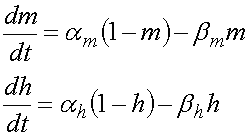


tengo una pregunta, cuando se calcula la corriente de sodio usando las ecuaciones de hyh, se ve que esta aumenta en el tiempo, luego de cae, y despues vuelve a aumentar y a bajar. es decir tiene forma de pico, y ddespues de panza. esto me hace ruido ya que no es lo que se ve en los registros electrofisiologicos. queria saber por que podia ser esta discrepancia, si tiene que ver con como se realizan los experimentos de voltage clamp, y si de verdad la corriente de sodio dura tanto.. gracias
ResponderEliminarBueno, respecto a tu pregunta te puedo aportar con algunos datos. En realidad la corriente de sodio de los canales activados por voltaje es rápida, es decir, los canales se abren rápidamente frente a una despolarización de la membrana, sin embargo, la activación de los canales de sodio dura poco tiempo pues presentan inactivación y luego de algunos milisegundos, la corriente de sodio se comienza a reducir hasta el 1%. Si ves la figura 2, puedes ver cómo aumenta h, lo que me imagino que es la panza que mencionas en la pregunta, sin embargo, esa curva representa la inactivación del canal. Recuerda que en el modelo de H-H “m” controla la activación, mientras que una partícula “h” es la encargada de la inactivación del canal. Respecto a las diferencias entre las cinéticas de los esquemas frente a los obtenidos en tus registros, se me ocurre que una causa puede ser la duración y magnitud de los pulsos que estás aplicando. Espero haber entendido bien la pregunta. De todos modos, si las dudas persisten, insiste y vuelve a preguntar. Saludos.
ResponderEliminarhola!! he leido acerca de la repolarizacion y despolarizacion, pero son conceptos que no me quedan claros, podrias ayudarme por favor?
ResponderEliminarMuy resumidamente, la membrana en reposo siempre presenta una diferencia de potencial entre el lado interno y el externo. El valor de este potencial de membrana oscila aproximadamente entre -60 mV a -70 mV. Cuando una célula recibe un estímulo, determinados canales iónicos se abren provocando un flujo neto de iones a través de su poro con lo que se altera el potencial de membrana en reposo y el valor del potencial de membrana se vuelve más positivo, por ejemplo -55 mV. Así, a este cambio (más positivo) en el potencial de membrana le llamamos despolarización. Estas despolarizaciones son muchas veces pasivas. Sin embargo, cuando la despolarización se aproxima a un nivel crítico llamado umbral, la célula responde activamente con la apertura de los canales iónicos sensibles a voltaje, generando un potencial de acción. La repolarización es el regreso al potencial de membrana de una célula en reposo, es decir, el regreso a un potencial entre -60 a -70 mV. Esto se consigue por ejemplo, con el cierre de canales de sodio.
EliminarEspero haberte ayudado. De todos modos, siento el retraso. Saludos y gracias por compartir tu inquietud.