Como pudiste ver en la entrada Potencial de membrana, su valor se encuentra determinada por los flujos de sodio y potasio. Es cierto que cuando la célula está en reposo, el potencial de membrana se acerca muchísimo al potencial de equilibrio del potasio y cuando se genera el potencial de acción, es el ion sodio el que influye mayormente en el potencial, sin embargo,sus valores no son exactamente igual a los potenciales de equilibrio de estos iones.
Si utilizamos la ecuación de Nernst para medir el potencial de membrana, tendremos que basarnos en la concentración intra y extracelular de un ion en particular lo que podría ser válido para el caso de la glia. Sin embargo, cuando el Vm (potencial de membrana) es determinado por más de una clase de iones, la influencia de cada una de ellas no se determina solamente por la diferencia en sus concentraciones, si no también por la permeabilidad de la membrana para tal o cual ion. La permeabilidad se mide en unidades de velocidad, o sea, cm/s. Esta medida es similar a la de una constante de difusión que mide el índice de movimiento de un soluto en una solución.
La dependencia del potencial de membrana respecto a la permeabilidad y a la concentración iónica viene determinada por la ecuación de Goldman:
La dependencia del potencial de membrana respecto a la permeabilidad y a la concentración iónica viene determinada por la ecuación de Goldman:
donde Vr es el potencial de reposo (en voltios), P es la permeabilidad para cada ión, [X]e es la concentración extracelular para cada ión y [X]i es la concentración intracelular para cada ión.
IMPORTANTE: esta ecuación se aplica sólo en condiciones de equilibrio, es decir, cuando el potencial de membrana, Vm, no está cambiando e indica que cuanto mayor es la concentración de un clase de ion en particular y cuanto mayor es la permeabilidad de la membrana para ella, tanto mayor es su importancia en la determinación del potencial de membrana.
En situaciones límite, por ejemplo potencial de reposo o potencial de acción (en el pico del potencial de acción hay un momento en el que Vm no varía) la ecuación de goldmann se puede reducir a la ecuación de Nernst, sin embargo, no hay que dejar de recordar que eso sería sólo una aproximación.
Por ejemplo, en el caso del potencial de reposo, los iones sodio y cloruro son poco determinantes en el Vm ya que la permeabilidad de la membrana por estos iones es muy baja comparada a la existente por potasio, por lo que nos podemos quedar sólo con los valores del potasio. De este modo, tenemos que:
Los razón de los valores de permeabilidad para el potasio, por supuesto equivalen a uno, por lo tanto no se escriben en la ecuación de Nernst.
Para el caso de la membrana en reposo, los índices de permeabilidad para los iones serían:
tomando como 1 la permeabilidad al potasio por ser la mayor y las demás en relación con ésta. Por esta razón, el potencial de reposo de la membrana se acerca al potencial de equilibrio del potasio.
Por otra parte, durante el potencial de acción, las permeabilidades de sodio varían, aumentando considerablemente con respecto al reposo y también a los demás iones, razón por la que el Vm se acerca al potencial de equilibrio del sodio. Por lo tanto, durante el potencial de acción los índices de permeabilidad serían:
En la práctica, se utiliza la permeabilidad en la ecuación de Goldman, mientras que se emplea la conductancia en las mediciones eléctricas y en los circuitos equivalentes.
La ecuación de Goldman no aporta información sobre los cambios del potencial de membrana en respuesta a un estímulo, ya que esta ecuación no se aplica más que al estado en equilibrio, en el que no hay cambios de voltaje.



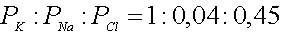

Podrias resolver la ecuación? Según el libro de fisiología humana del autor Guyton sale -86mv. Quiero saber los valores porfavor. Gracias
ResponderEliminarHola,
ResponderEliminarContestando a tu pregunta, te puedo señalar que el valor del potencial de reposo que obtengas pueden variar según las concentraciones de iones que tengas fuera y dentro de la células, pero este valor siempre se acercará más al potencial de equilibrio del potasio, que al de cualquier otro ion.
Al final de esta entrada http://acercandolabiofisica.blogspot.com/2009/10/potenciales-de-equilibrio-y-ecuacion-de.html , podrás ver las tablas con los valores referenciales para la concentración de iones intra y extracelular tanto para el músculo esquelético como para el axón gigante de calamar.Es importante que recuerdes que sólo se trata de una referencia.
Ahora, recuerda que los índices de permeabilidad para el sodio y el cloruro durante el reposo, son tan bajos que se pueden despreciar, ahora si quieres hacer el cálculo más exacto, los puedes incluir. El valor de las razones de permeabilidad están en esta entrada.
Para resolver la ecuación, considera la razón de permeabilidad del potasio igual a 1 y reemplazas el valor de RT/ZF (25,69 a 25 °C) y los valores del potasio externo y del potasio interno que aparecen en las tablas. Con eso te dará un valor parecido al los -86 mV. Como te dije estos valores variarán según el tipo de célula y su composición iónica, pero debería ser cercano al potencial de reposo del potasio.
Muchas gracias amigo esta excelente, pero podrías por favor poner las referencias, sobre todo me interesa saber de dónde obtuviste las proporciones de las permeabilidades en el potencial de reposo y el potencial de acción.
ResponderEliminarHola,
Eliminarte adjunto el link del artículo original: The effect of sodium ions on the electrical activity of the giant axon of the squid. A. L. Hodgkin and B. Katz. J. Physiol. 1949;108;37-77
http://www.sci.utah.edu/~macleod/bioen/be6003/notes/W02-Hodgkin-Katz49.pdf
Si necesitas más material, avísame que he vuelto a retomar el blog :)
Saludos!
Muchas gracias jeje el próximo semestre inscribiré biofísica =)
Eliminardisculpa me podrías ayudar con esta pregunta
ResponderEliminar¿Cual de los parámetros en la ecuación de Goldman-Hodgkin-Katz cambia
cuando una molécula de neurotransmisor se une a un receptor postsináptico y
abre canales iónicos dependientes de ligando?
Lo que cambia es la permeabilidad. Por ejemplo, en el caso de la acetilcolina, la unión de esta molécula a cada uno de los dos sitios fijadores de ACh ubicados en la subunidad alfa, genera un cambio conformacional en la proteína, favoreciendo de este modo la apertura del canal y permitiendo entonces, el flujo de Na+ y K+ a través de su poro. Si las moléculas de acetilcolina no están unidas al receptor, este flujo no se produce ya que el canal está cerrado.
EliminarGracias por tu pregunta, la verdad es que me motivó a escribir una nueva entrada. Espero subirla próximamente. Saludos!
Me han encantado tus explicaciones! Sos sumamente claro y práctico! Felicitaciones!
ResponderEliminar